Unit 8.2 Exponential Functions and Half Life
Exponential Functions
Exponential functions are a class of functions that grow or decay at a rate proportional to their current value. They are widely used in various fields such as mathematics, physics, engineering, and economics to model growth and decay processes.
Definition
An exponential function models growth or decay that is non-continuous. Meaning that it occurs after an event has occurred. A yearly interest rate would be an example
f(x) = a ⋅ bc⋅x
Where:
- a is a constant called the initial value or the coefficient.
- b is the base of the exponential function, a positive real number.
- c represents growth or decay (positive or negative) and the rate which it grows or decreases
- x is the exponent, which is a real number.
Another way to write non-continuous exponential functions, particularly for finance is
PF = P0 (1 + r)t (growth)
PF = P0 (1 - r)t (decay)
Where
- PF = final population
- P0 = initial population
- r = rate of growth or decay
- t = the amount of time
Properties
Growth and Decay
If b > 1 the function represents exponential growth.
If 0 < b < 1, the function represents exponential decay.
If c > 0, the function represents exponential growth
If c < 0, the function represents exponential decay
Asymptotes
The horizontal asymptote of f(x) = a ⋅ bc⋅x is the line that the functions will get closer and closer to but never cross.
Examples of Exponential Graphs
f(x) = 2x
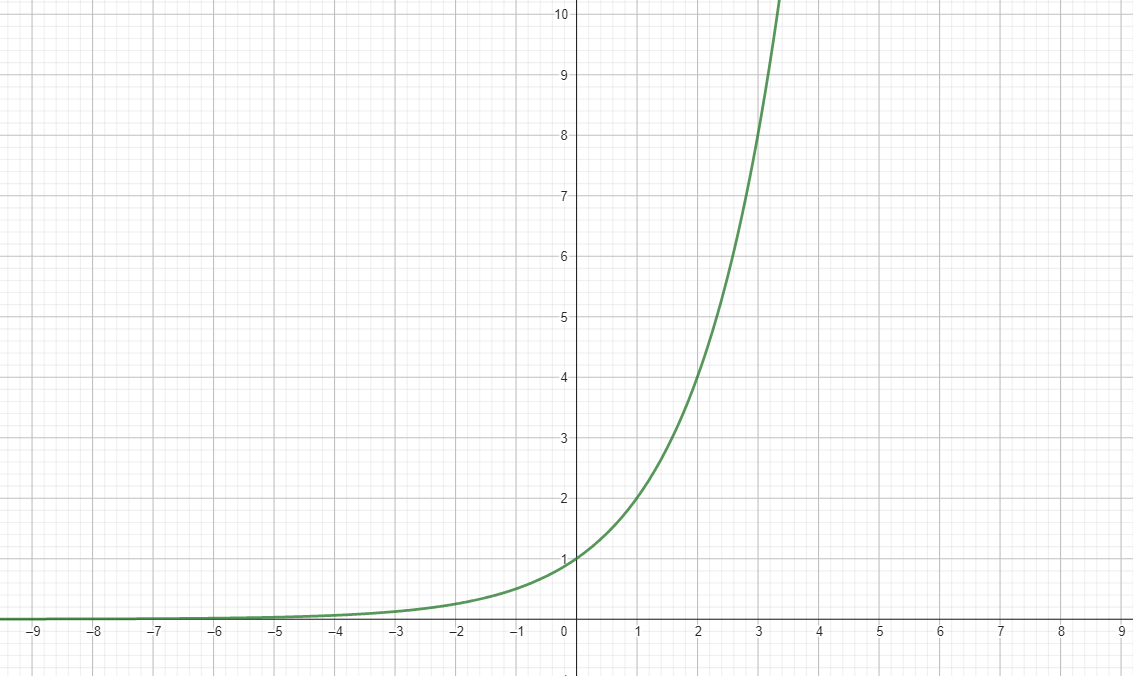
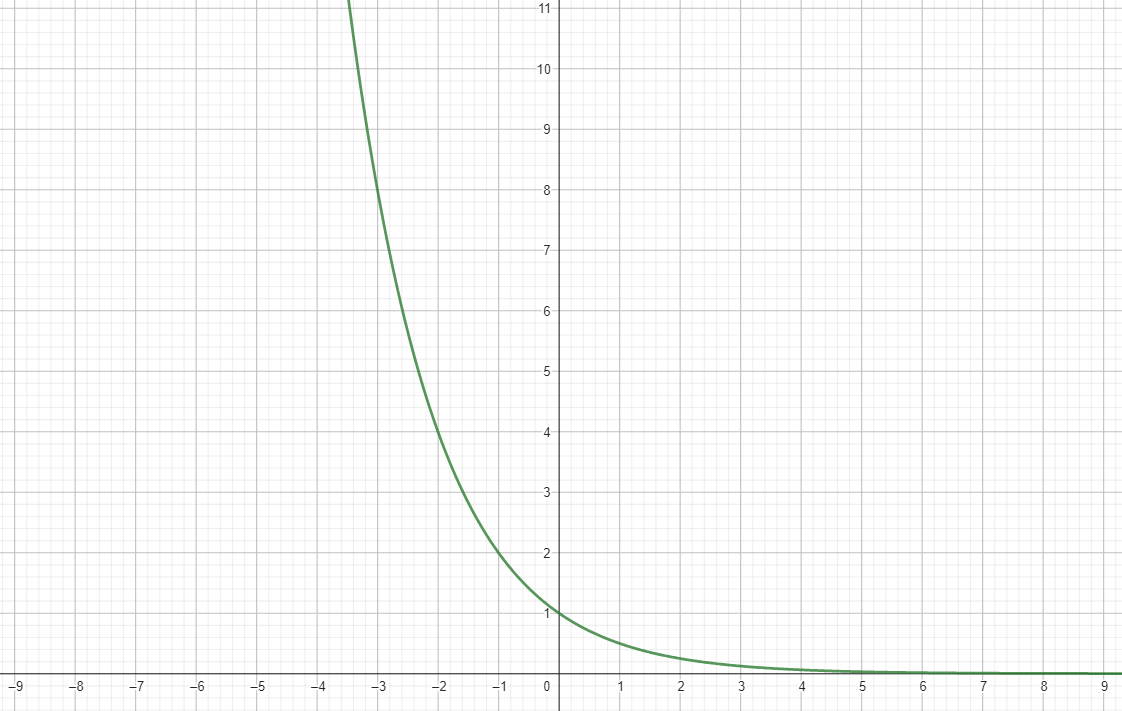
f(x) = 0.5x
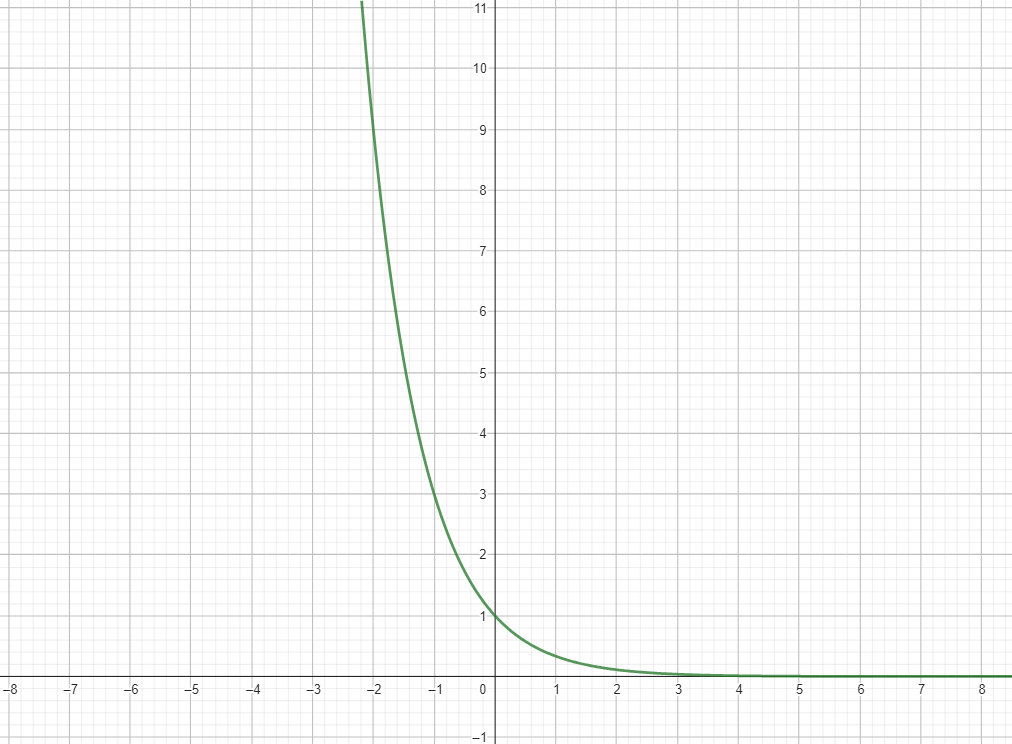
f(x) = 3-x
Half Life
The concept of half-life is crucial in fields such as physics, chemistry, biology, and pharmacology. It describes the time required for a quantity to reduce to half its initial value. This concept is most commonly applied to the decay of radioactive substances, but it also applies to other processes like chemical reactions and the elimination of drugs from the body.
The half-life (t1/2) of a substance is the time required for half of the substance to decay or be reduced to half its initial amount.
The half life function can be described as
[latex]N(t) = N_0 \left(0.5\right)^{\frac{t}{t_{1/2}}}[/latex]
Where
- N(t) is the final amount
- N0 is the initial amount
- t is the amount of time passed
- t1/2 is the half life
Half Life Equation
Californium-252 is used to inspect airline luggage for hidden explosives and for reactor startup. It has a half life of 2.645 years. How much will be left if you originally had a 3 mg sample after 10 years?
N(t) = 0.003 (0.5)10/2.645
N(t) = 0.00022 g
N(t) = 0.2 mg