Functions

A function describes a relationship between two sets, typically referred to as the domain and the range. A function assigns each element in the domain to exactly one element in the range. (See 4.6 for a function recap)

You can write instructions for functions multiple different ways

Multiplication: f(x) · g(x)

Division: [latex]\frac{f(x)}{g(x)}\ \ or\ \ f(x)\ \div\ g(x)[/latex]

Addition and Subtraction: f(x) + g(x)

Function of a function: f(g(x)) or f ◦ g (x)

Inverse of Functions

Functions that are one-to-one have inverses. An inverse function essentially reverses the assignment of a function. Usually denoted by f ^-1 (x). The inverse of a function is where the domain and ranges are swapped.

For example, if you had a set of x values (domain) that were

x = {1,2,3}

and y values (range) that were

y = {4,5,6}

to find the inverse, swap the x and y values

x = {4,5,6} and y = {1,2,3}

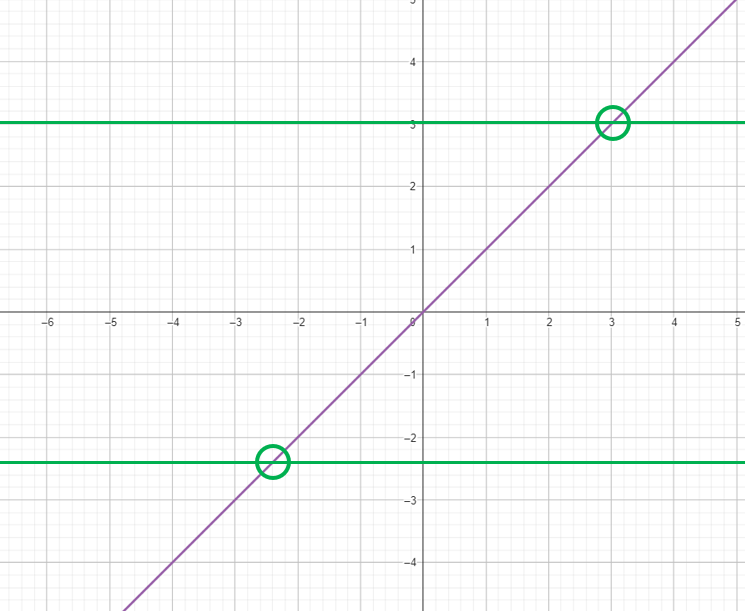
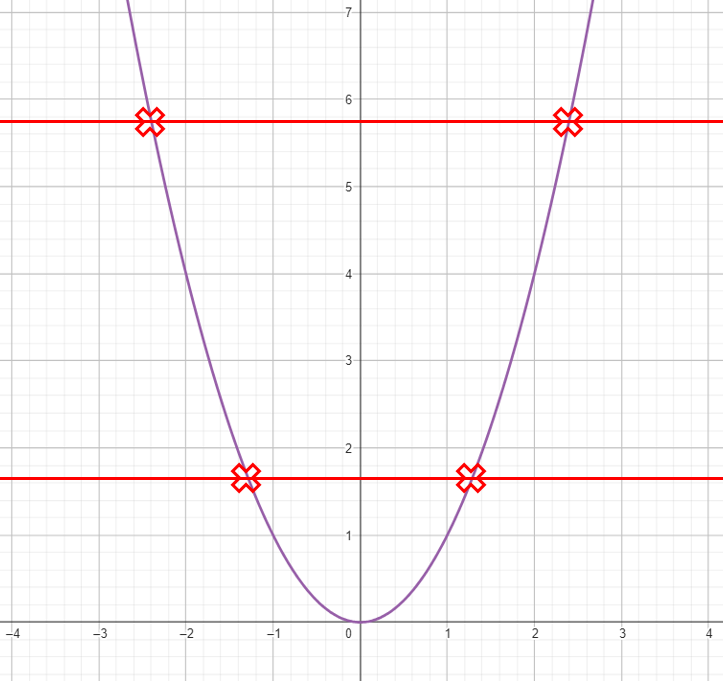
One way to tell if a function has an inverse, is using the horizontal line test. Like the vertical line test, except the lines are drawn horizontally. If the horizontal crosses the graph more than once, it will not have an inverse

y = x  has an inverse                                                                  y = x² does NOT have an inverse

Finding the Inverse of a Function

To find the inverse of a function, swap the x and y values, and solve for y