Unit 7.4 Converting Between Polar and Rectangular
Polar Format
Complex numbers can also be represented in polar form, which provides an alternative to the standard rectangular form a + bi The polar form emphasizes the magnitude and direction of the complex number.
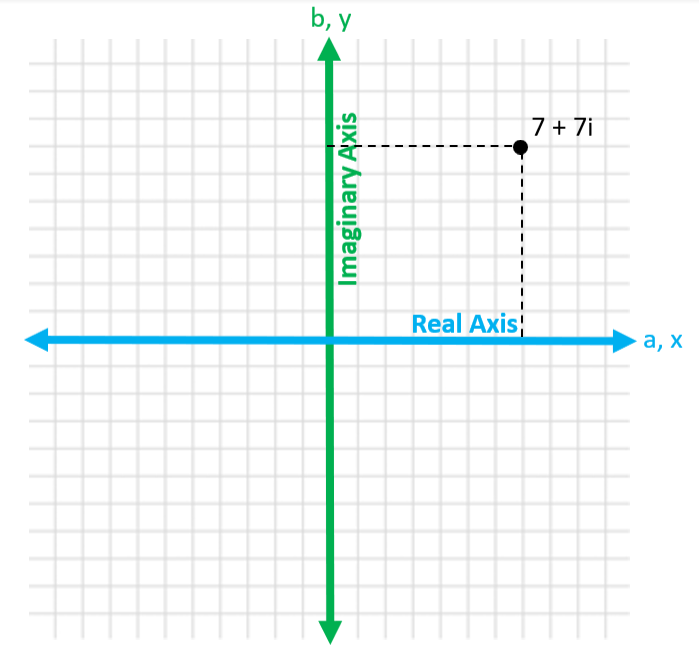
Take the point 7 + 7i, in rectangular format, we move over 7 on the real axis and up 7 on the imaginary.
x is the real component and y is the imaginary component
There is another way to represent this point on the graph. That is to have a line that starts at the origin and extends a certain length (r) at a certain angle (θ)
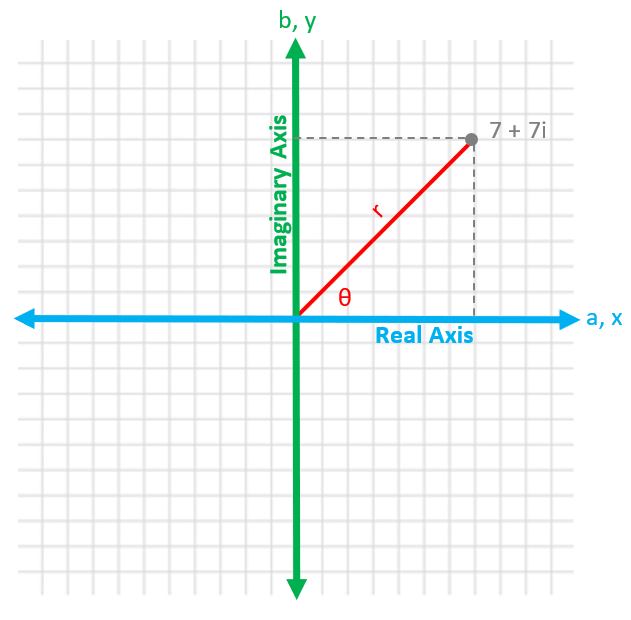
This is called Polar Format
Polar Format
r ∠ θ
Where r is the magnitude (or modulus) of the complex number
θ is the argument (or angle) of the complex number and is in degrees
Converting Between Polar and Rectangular
Looking at the graph, we can see that it forms a right triangle
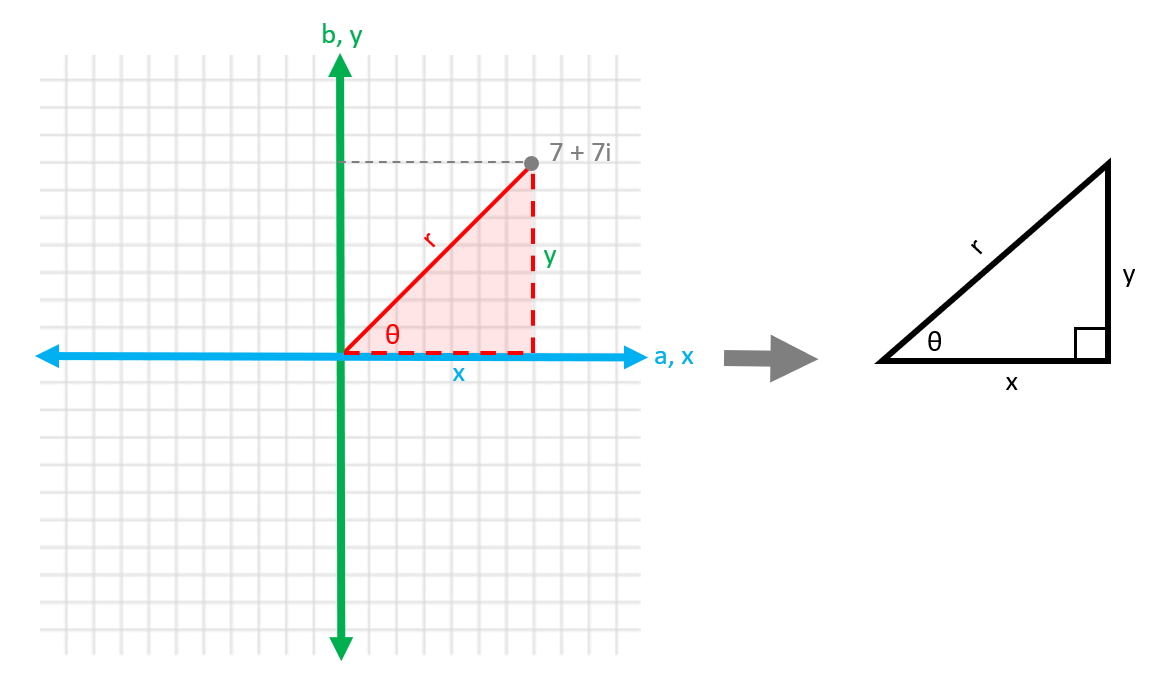
With the imaginary component "y" being one side, the real component "x" being one side and r is the hypotenuse.
Converting to Polar
Given the values for x and y, in rectangular format, we are able to use Pythagoreans Theorem to find the hypotenuse
x2 + y2 = r2
[latex]r=\ \sqrt{a^2+b^2}\ \ \ \ or\ \ \ \ \ \sqrt{x^2+y^2}[/latex]
Given the values for x and y, in rectangular format, we can use trigonometry to find θ. Remember SOH CAH TOA. We have both the opposite side, and adjacent side, so we use tangent
[latex]\theta=\tan^{-1}{\left(\frac{b}{a}\right)}\ \ \ or\ \ \ \ \ \tan^{-1}{\ \left(\frac{y}{x}\right)\ }[/latex]
Converting to Rectangular
If we have r and θ but not x and y, we can use trigonometry to find x and y
Remember SOH CAH TOA. Given that we have the hypotenuse, and an angle, we are able to use sine and cosine to find x and y.
[latex]sin\ \theta\ =\ \frac{opposite}{hypotenuse}=\frac{y}{r}[/latex]
[latex]b=\ r\ \ast\sin{\left(\theta\right)\ \ \ \ \ or\ \ \ \ y=\ r\ \ast\sin{\left(\theta\right)\ \ \ \ \ }\ }[/latex]
Remember to include the "i" on the imaginary component
[latex]cos\ \theta\ =\ \frac{adjacent}{hypotenuse}=\frac{x}{r}[/latex]
[latex]a=\ r\ \ast\cos{\left(\theta\right)\ \ \ \ \ or\ \ \ \ x=\ r\ \ast\cos{\left(\theta\right)\ \ \ \ \ }\ }[/latex]