Unit 7.2 Introduction to Complex Numbers and Addition
Complex Numbers
Complex numbers are an extension of the real numbers and are used in various fields, including engineering, physics, and mathematics. They provide a way to solve equations that have no real solutions
Complex numbers can take this format, called rectangular format
Rectangular Format
a + bi or x + yi or x + jy
Where "a" and "x" are real numbers and "b" and "y" are imaginary. They have an "i" or "j" attached to denote the imaginary component
What is "i"?
"i" (sometimes "j" in electronics) is the representation of the imaginary value of [latex]\sqrt{-1}[/latex]
It can be used to denote any value that results from taking the root of a negative number
Taking the Root of a Negative Number
[latex]\sqrt{-25}=\ \sqrt{25}\cdot\sqrt{-1}\ =\ 5\cdot i=5i[/latex]
If you have i2 it equals -1 ([latex]\left(\sqrt{-1}\right)^2=-1[/latex])
All imaginary components to a power can be simplified this way. For example if you had i3 it would equate to [latex]\left(\sqrt{-1}\right)^3=-1\ \cdot\ \sqrt{-1}\ =\ -i[/latex]
Adding Complex Numbers
In the same way that x and y cannot be added together, real numbers and complex numbers cannot be added. It must remain in one of the formats listed above. You can add real numbers and real numbers or imaginary or imaginary.
Adding Complex Numbers
[latex](5\ +\ 2i)+(3\ +\ i)=(5+3)+(2i\ +\ i)=8+3i[/latex]
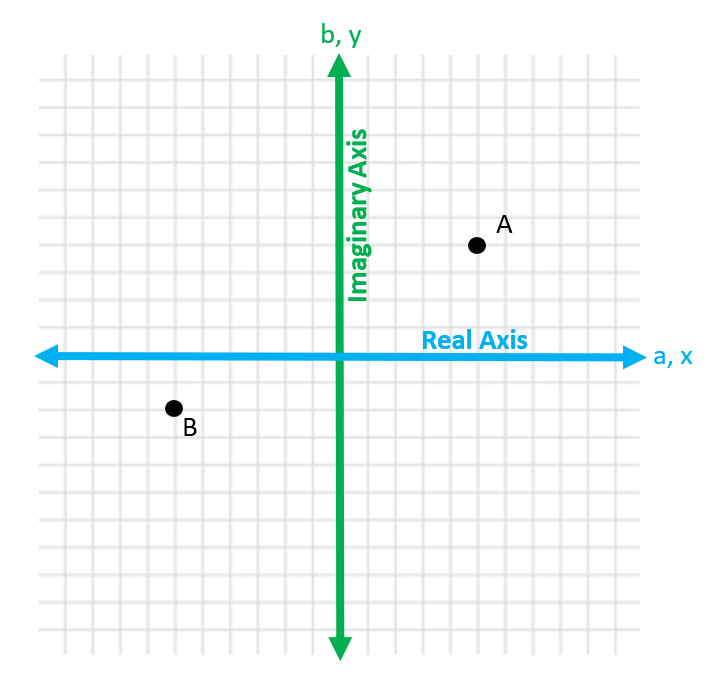
Graphing Complex Numbers
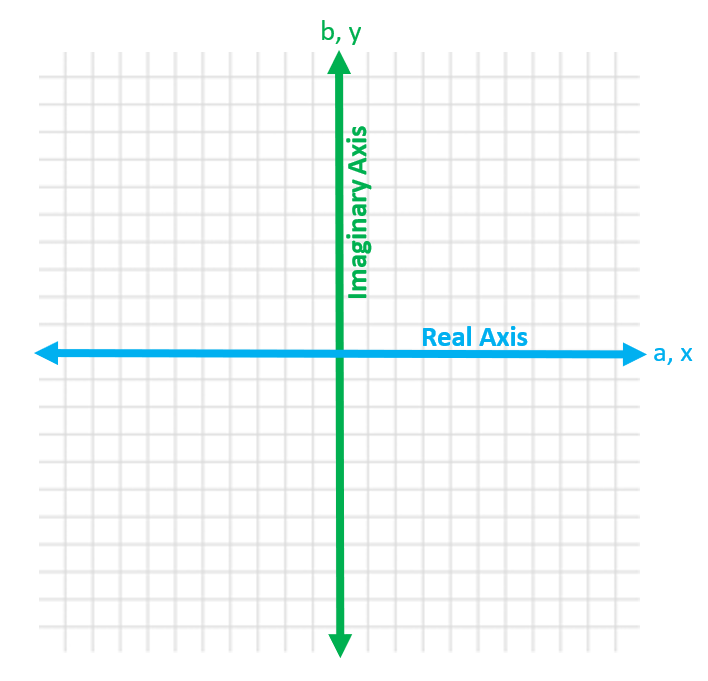
When graphing with imaginary numbers, the vertical axis is the imaginary axis and the horizontal axis is the real axis.
A complex number in rectangular format gives us the coordinates to be plotted on the graph. For example, 2 + 3i means that it is 2 over on the real axis, and up 3 on the imaginary
Graphing Complex Numbers
Graph 5 + 4i (A) and -6 - 2i (B)