Unit 5.5 Introduction to Polynomial Factoring
Polynomial Factoring
When you multiply 2 polynomials together you get a larger polynomial. Polynomial factoring undoes this action to be able to determine the two smaller polynomials that were originally multiplied together. You can factor out two polynomials or even a monomial from a larger polynomial.
Factoring a Polynomial with a leading coefficient of 1
Fully factor x2 + 8x + 12
When looking at this polynomial, we are looking for two numbers that multiply to a positive 12 and add to a positive 8
List all the factors of 12: (1,12) (2,6) (3,4)
Out of all the factors, 2 and 6 add up to 8
Therefore, the factored binomials are (x + 2) and (x + 6)
helpful hint: You can check your work by multiplying the two back together and you should get x2 + 8x + 12
- When both the second and third terms are positive, the values are going to be positive
- When the second term is negative and the third is positive, both values are negative
- When the third term is negative, only one of the values is negative
Factoring a Polynomial with a leading coefficient greater than 1
Fully factor 4x2 – 19x – 5
We cannot neglect the 4 coefficient, therefore we need to use the AC method
We multiply the value of A (4) by the value of C (-5) to get a resulting value
4 ⋅ -5 = -20
Then we find a factor of -20 that add to a -19
Factors of 20: (1,20) (2,10) (4,5)
Looking at the factors of 20, we can see that if we added -20 and a positive 1, we would get -19
Break apart the -19x into component parts
4x2 – 20x + 1x – 5
The value of our expression did not change, just took on a different format
We can then do what is called factor by grouping. Group the expression together in pairs that can be factored
(4x2 – 20x) + (x – 5)
Then factor out the monomials accordingly
4x (x – 5) + (x – 5)
We want the two binomials that are left to match. They do in this case so we are able to move the 4x and 1 into their own binomial
4x (x – 5) + 1(x – 5)
(4x + 1) (x – 5)
The two binomials that 4x2 – 19x – 5 factor into are (4x + 1) (x – 5)
Solving for Roots
Roots are mathematical expression used to describe where a function crosses the x axis. For linear equations, the highest order power is 1, therefore it only crosses the axis 1 time. For a polynomial with a highest exponent of 2, it will cross the axis 2 times. Part of solving for roots means that factoring is required, and that the expression is set equal to zero.
Solving for roots
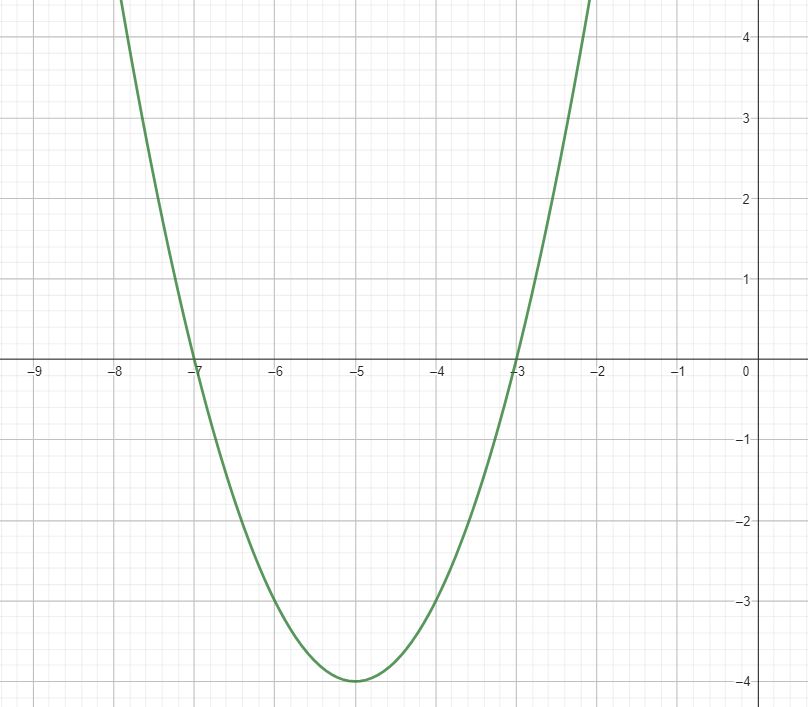
Find the roots of x2 + 10x + 21 = 0
First factor the equation
When looking at this polynomial, we are looking for two numbers that multiply to a positive 21 and add to a positive 10
List all the factors of 21: (1,21) (3,7)
The factors that add to a positive 10 are 3 and 7
(x + 7) (x + 3) = 0
Set each of the binomials equal to zero
(x + 7) = 0 (x + 3) = 0
Solve for x
x = -7 x = -3
The roots of this polynomial are -7 and -3
If we were to graph this polynomial, we would see that the function crosses the x axis 2 times at -3 and -7