Unit 4.6 Introduction to Functions
Functions
Functions are relations between sets of inputs (x) and outputs (y). Often these inputs and outputs are called domain and ranges.
Where x values are domain values and y values are range values. These are the values where the equation is defined. An equation is only a function if each input has exactly one output.
y = x is a function because if you plug in an x value, you get exactly 1 y value.
y = ± x is not a function because x could be positive or negative. giving two different y values.
Functions
Example 1:
For the ordered pairs (1,2) (5,4) (7,8) and (3, 4), does this represent a function?
List and group all x and y values
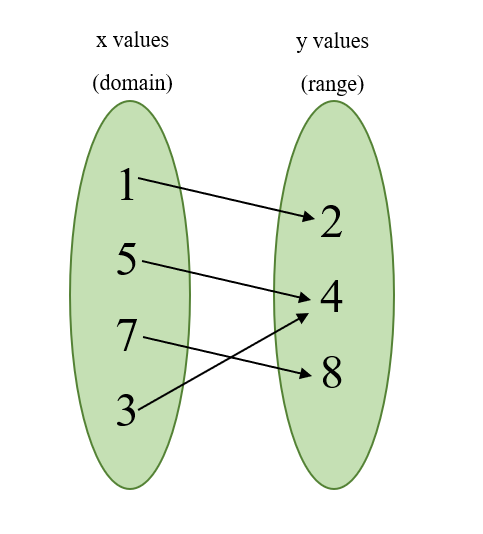
Because each x value is unique, and only has one y value (one arrow), these ordered pairs represent a function
Example 2:
For the ordered pairs (1,5) (1,4) (4,4) (6, 7) does this represent a function?
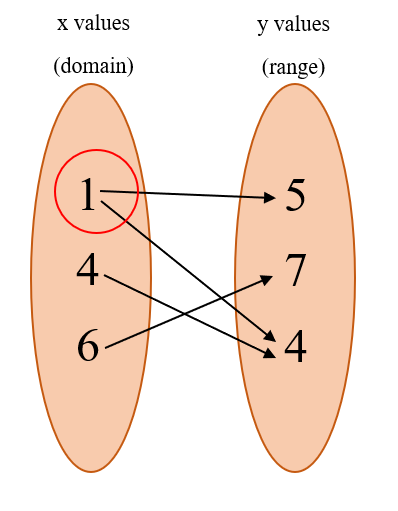
Because one of our x values has two arrows, i.e. it has two y values, it is not a function
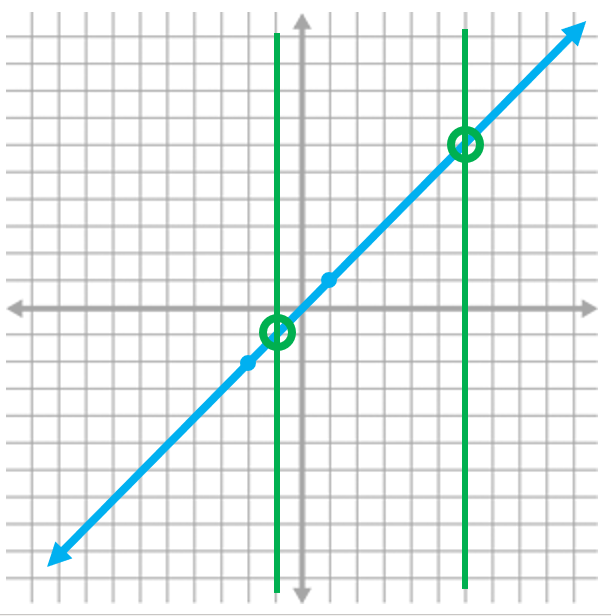
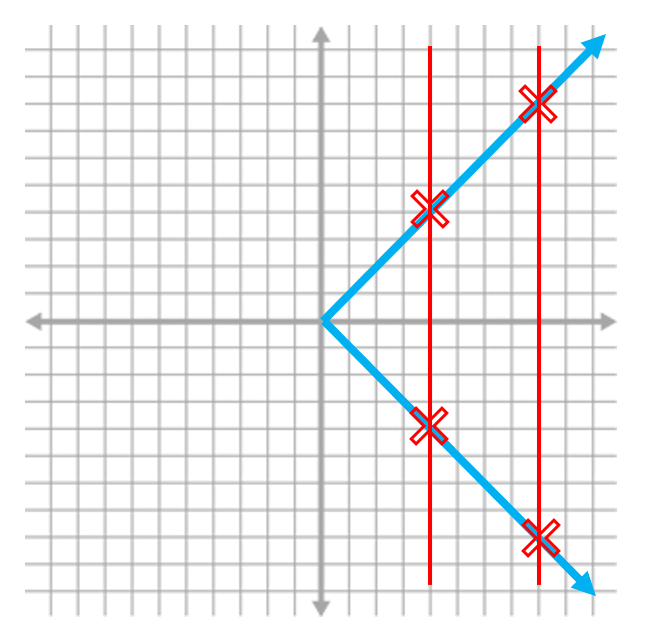
One way to tell if an equation is a function is to do a “vertical line test”. You draw a vertical line through your graph. If it crosses the shape more than once, it is NOT a function
Function Not a Function
Function Notation
Functions are often notated using function notation.
f(x) = x
this is no different than saying
y = x
We replace the “y” with the value “f(x)”. In this case we are saying that “f” is a function of “x”. It can be any letter combination so long as the “x” is a defined variable within the function
For example:
h(a) = a + 1
h is a function of a, where a is the variable