Unit 14.2 Solving Systems of Equations using Matricies
Solving Systems of Equations using the Matrix Method
Matrices can be used to express systems of equations as well. For example, if you had a systems of equations
2x - y + z = 4 (eq. 1)
x + 3y - 2z = -6 (eq. 2)
3x - 2y + 4z = 10 (eq. 3)
Putting these equations into a matrix where the rows represent the equations and the columns represent the variables. You are only concerned with the coefficients on each of the variables.
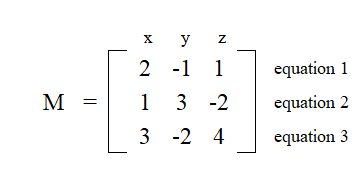
The "constant" matrix (C) would be the values that are constants on the other side of the equals sign
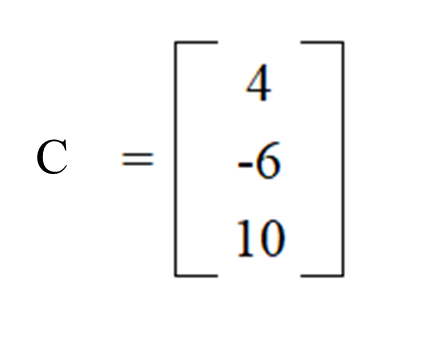
You then multiply M by the variable matrix to get our solution. This is how you set up a matrix to solve for x, y and z
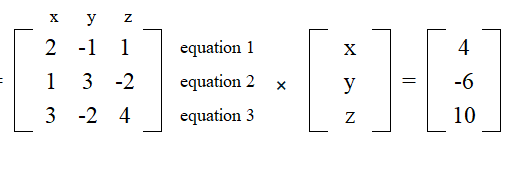
If this was a ordinary linear equation where you were solving for x, C = Ax then you would solve for x by multiplying the constant (C) by the inverse of A. so x = [latex]\ C \cdot\frac{1}{A}[/latex]. This is also true for matrices.
[latex]\left[\begin{matrix}x\\y\\z\\\end{matrix}\right]=C\cdot M^{-1}[/latex]
So to solve for x, y and z, we would multiply the constant matrix (C) by the inverse of M (M -1)
Solving a systems of equations using the matrix method
Given the systems of equations
[latex]\begin{matrix}2x+6y=5\\x+4y=3\\\end{matrix}[/latex]
Solve using the matrix method
Start by setting up your matrices. Remember to line up your like values and you are only concerned with the coefficients on the variables
[latex]M=\left[\begin{matrix}2&6\\1&4\\\end{matrix}\right][/latex] and [latex]\ C=\left[\begin{matrix}5\\3\\\end{matrix}\right][/latex]
Set up your equation
M [latex]\cdot\left[\begin{matrix}x\\y\\\end{matrix}\right][/latex] = C
[latex]\left[\begin{matrix}2&6\\1&4\\\end{matrix}\right]\cdot\left[\begin{matrix}x\\y\\\end{matrix}\right]=\left[\begin{matrix}5\\3\\\end{matrix}\right][/latex]
Then
[latex]\left[\begin{matrix}x\\y\\\end{matrix}\right]=C\cdot M^{-1}[/latex]
To find the inverse of a 2x2, first find the determinate of M
[latex]det=ad-bc=\left(2\cdot4\right)-\left(6\cdot1\right)=2[/latex]
Multiply 1/det by the transpose of matrix M to get the inverse
[latex]M^{-1}=\frac{1}{det}\left[\begin{matrix}d&-b\\-c&a\\\end{matrix}\right]=\frac{1}{2}\left[\begin{matrix}4&-6\\-1&2\\\end{matrix}\right]=\left[\begin{matrix}2&-3\\-\frac{1}{2}&1\\\end{matrix}\right][/latex]
Multiply the inverse of M by S to get our solutions for x and y
[latex]\left[\begin{matrix}x\\y\\\end{matrix}\right]=C\cdot M^{-1}[/latex]
[latex]\left[\begin{matrix}x\\y\\\end{matrix}\right]=\left[\begin{matrix}5\\3\\\end{matrix}\right]\cdot\left[\begin{matrix}2&-3\\\frac{1}{2}&1\\\end{matrix}\right]=\left[\begin{matrix}\left(5\cdot2\right)+\left(3\cdot-3\right)\\\left(5\cdot-\frac{1}{2}\right)+\left(3\cdot1\right)\\\end{matrix}\right]=\left[\begin{matrix}1\\\frac{1}{2}\\\end{matrix}\right][/latex]