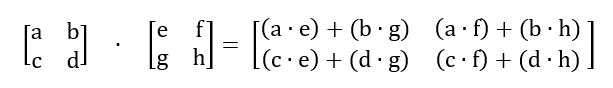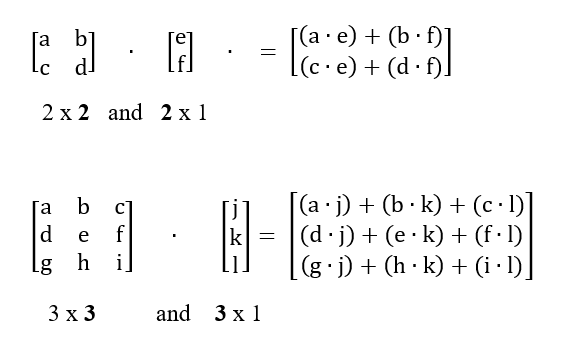Unit 14.2 Matrices
Introduction to Matrices
A matrix is a rectangular array of numbers, symbols, or expressions arranged in rows and columns. Matrices are used in various fields such as mathematics, engineering, physics, and computer science to represent data, solve systems of linear equations, and perform transformations. They are another way to express and solve systems of equations
Matrices can take the format (keep in mind that there are many other forms matrices can take)
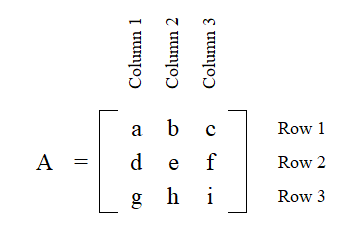
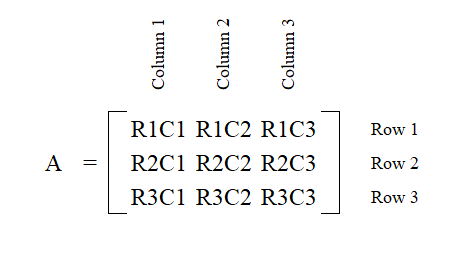
Where the letters are stand in for numerical values. The horizontal are called "rows" and the vertical are called "columns". It is read from left to right. Each numerical value has an "address" within the matrix. Rows are always listed first. For example "a" would have an address of Row 1 Column 1 (R1C1)
Matrix A would be a 3x3 matrix because it has 3 rows and 3 columns. Matrix B would be a 2x2 matrix since it has two rows and two columns and Matrix C would be a 1x2 matrix since it has 1 row and 2 columns. When the number of rows and columns match, it is considered a "square" matrix
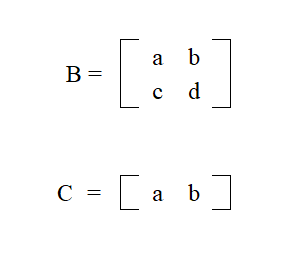
Adding Matrices
To add matrices together, the number of rows and columns need to match, (i.e they have the same "dimensions"). Then add R1C1 of one matrix with R1C1 of the other. Continue down the rows and columns
Adding Matrices
Looking at matrix A and B, find A + B
[latex]A\ =\left[\begin{matrix}1&2&3\\6&5&4\\7&8&9\\\end{matrix}\right]\ \ \ \ \ \ \ \ \ B\ =\left[\begin{matrix}8&7&6\\5&4&3\\2&1&0\\\end{matrix}\right][/latex]
Since both matrices have 3 rows and 3 columns, we can add them. Add R1C1 of A to R1C1 of B and then continue with each value
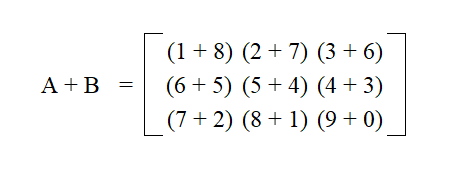
Simplify
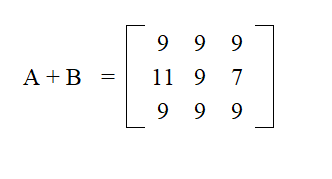
Multiplying Matrices
Multiplying matrices by a scalar (a single number) doesn't require any special parameters. Multiply each value in the matrix by the scalar
Multiplying by a scalar
Looking at the matrix A, find 3A
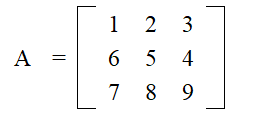
Multiply each value by 3

Simplify
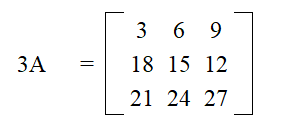
Multiplying two matrices together is more involved. Before multiplying two together, confirm that the number of columns in the first matrix matches the number of rows in the second
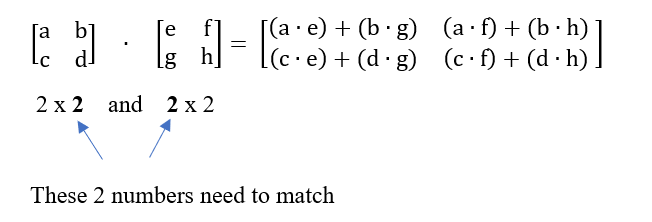
To multiply two together, multiply each value in the first row (of the first matrix) by the first column (of the second matrix) and add
Multiplying a 2x2 by a 2x1
Multiply A = [latex]\left[\begin{matrix}1&2\\3&4\\\end{matrix}\right][/latex] by B = [latex]\left[\begin{matrix}5\\6\\\end{matrix}\right][/latex]
Verify that these two can be multiplied by comparing the columns of A by the rows of B. A is a 2x2 matrix and B is a 2x1. Since they are the same number, we can multiply
Multiply each of the rows in A by the first column in B then add. Multiply the second row in A by the column in B and add. Your result will be a 2x1 matrix
[latex]\left[\begin{matrix}1&2\\3&4\\\end{matrix}\right]\ \ \ \ \ \ \cdot\ \ \ \ \ \left[\begin{matrix}5\\6\\\end{matrix}\right]=\ \left[\begin{matrix}\left(1\cdot5\right)+\left(2\cdot6\right)\\\left(3\cdot5\right)+\left(4\cdot6\right)\\\end{matrix}\right]=\left[\begin{matrix}17\\39\\\end{matrix}\right][/latex]
Multiplying a 2x2 by a 2x2
Multiply A = [latex]\left[\begin{matrix}1&2\\3&4\\\end{matrix}\right][/latex] by B = [latex]\ \ \left[\begin{matrix}5&6\\7&8\\\end{matrix}\right][/latex]
Confirm that the two can be multiplied together by checking the columns by the rows. Since they are both 2x2 they match and can be multiplied
Multiply the first row in A by the first column in B then add. Then multiply the second row in A by the first column. This value will be in R2C1 of your new matrix. Repeat the process with the second column in B.
[latex]\left[\begin{matrix}1&2\\3&4\\\end{matrix}\right]\ \ \ \ \ \ \cdot\ \ \ \ \ \left[\begin{matrix}5&6\\7&8\\\end{matrix}\right]=\ \left[\begin{matrix}(1\cdot5)+(2\cdot7)\ &(1\cdot6)+(2\cdot8)\\(3\cdot5)+(4\cdot7)&(3\cdot6)+(4\cdot8)\\\end{matrix}\right]=\left[\begin{matrix}19&22\\43&50\\\end{matrix}\right][/latex]
Templates for Multiplication of Two Matrices