Unit 13.4 Practical Applications of Systems of Equations
Practical Applications of Systems of Equations
Systems of equations are a powerful tool in mathematics and have numerous real-world applications across various fields. Including physics, circuits, finance, chemistry, and even healthcare. These applications often involve situations where multiple conditions must be satisfied simultaneously, making systems of equations an ideal method for finding solutions.
These systems of equations are solved the same as any, but the key is in the setup of the equations
Real world systems of equations
Looking at the circuit below, find the voltages at node a and b (Va and Vb)
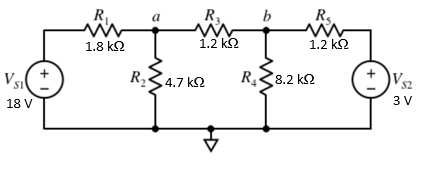
The derived equations from this circuit (using Kirchhoff's laws and Ohm's law) would be
[latex]\frac{3}{1.2}\ =\ \frac{17.6\ V_b}{9.84}\ -\ \frac{V_a}{1.2}[/latex] (eq. 1)
[latex]\frac{18}{1.8}\ =\ \frac{15.48\ V_a}{9.66}\ -\ \frac{V_b}{1.2}[/latex] (eq. 2)
Rewrite the equations so that the values are "lined up"
[latex]\frac{3}{1.2}\ =-\ \frac{1}{1.2}V_a\ +\ \frac{17.6\ }{9.84}\ V_b[/latex] (eq. 1)
[latex]\frac{18}{1.8}\ =\ \frac{15.48\ }{9.66}V_a\ -\ \frac{1}{1.2}V_b[/latex] (eq. 2)
You can simplify the fractions to decimal numbers (optional)
[latex]2.500\ =-\ 0.833\ V_a\ +\ 1.789\ V_b[/latex] (eq. 1)
[latex]\ 10.000=\ {1.602\ V}_a\ -\ 0.833\ V_b[/latex] (eq. 2)
Using elimination, solve for one of the variables. In this case we will eliminate Va by multiplying it by 1.923.
Equation 1:
[latex]1.923\ (2.500\ =-\ 0.833\ V_a\ +\ 1.789\ V_b)[/latex]
[latex]4.808\ =-\ 1.602\ V_a\ +\ 3.441\ V_b[/latex] (eq. 1a)
Add equation 2 to equation 1a to eliminate Va
[latex]\ \ \ \ \ \ 4.808\ =-\ 1.602\ V_a\ +\ 3.441\ V_b[/latex] (eq. 1a)
[latex]+\ \ 10.000=\ {1.602\ V}_a\ -\ 0.833\ V_b[/latex] (eq. 2)
_______________________________________________
14.808 = 2.608 Vb
Vb = 5.68 V
Plug Vb into one of the original equations to solve for Va
[latex]10=\ {1.602\ V}_a\ -\ 0.833\ V_b[/latex]
[latex]10=\ {1.602\ V}_a\ -\ 0.833\ (5.68)[/latex]
Va = 9.19 V
The voltage at node a (Va) = 9.19 V and the voltage at node b (Vb) = 5.68 V