Unit 13.1 Introduction to Systems of Equations and Graphing
Introduction to Systems of Equations
A system of equations is a set of two or more equations that have the same variables. The goal in solving a system of equations is to find the values of the variables that satisfy all the equations in the system simultaneously. Systems of equations can be solved using various methods, including graphing, substitution, and elimination.
When dealing with a systems of equations, it is important to understand that the number of unknown variables you have need to match the amount of equations you have. If you have 2 unknown variables (x and y) then you need 2 equations. If you have 3 unknown variables (x, y and z) then you need 3 equations.
Types of Solutions
- One Solution: If the system has one solution, the graphs of the equations intersect at a single point. This point represents the values of the variables that satisfy both equations.
- No Solution: If the system has no solution, the graphs of the equations are parallel and never intersect.
- Infinite Solutions: If the system has infinitely many solutions, the graphs of the equations coincide, meaning they are the same line.
Graphing Systems of Equations
One of the most visual ways to solve a system of equations is by graphing. The idea is to graph each equation on the same set of axes and then identify where the graphs intersect called a "solution"
Start by rewriting each equation in slope intercept form. Then graph the lines. Where they intersect is the solution of the systems of equations
Graphing Systems of Equations
Solve by graphing
[latex]\begin{aligned} y &= 2x + 3 \\ y &= -x + 1 \end{aligned}[/latex]
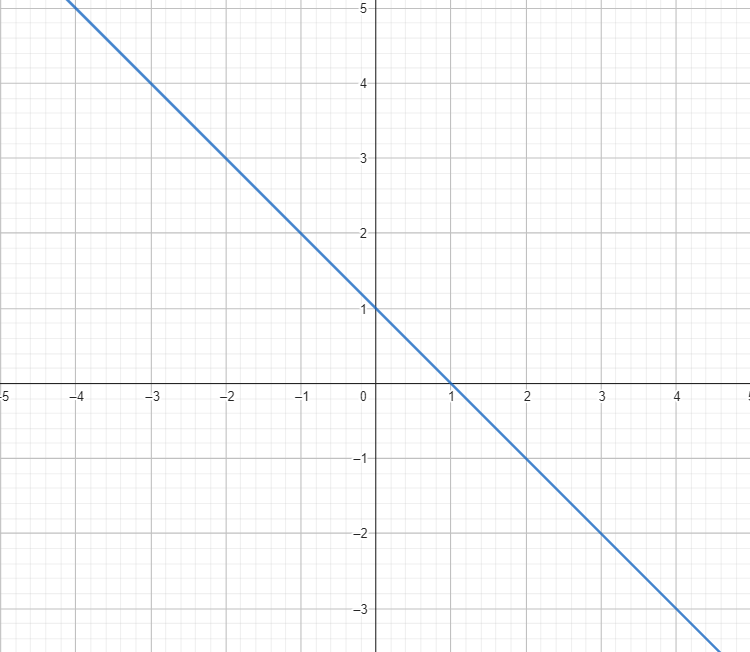
Graph the first line. Find two sets of ordered pairs
y = 2x + 3
(0,3) and (1,5)
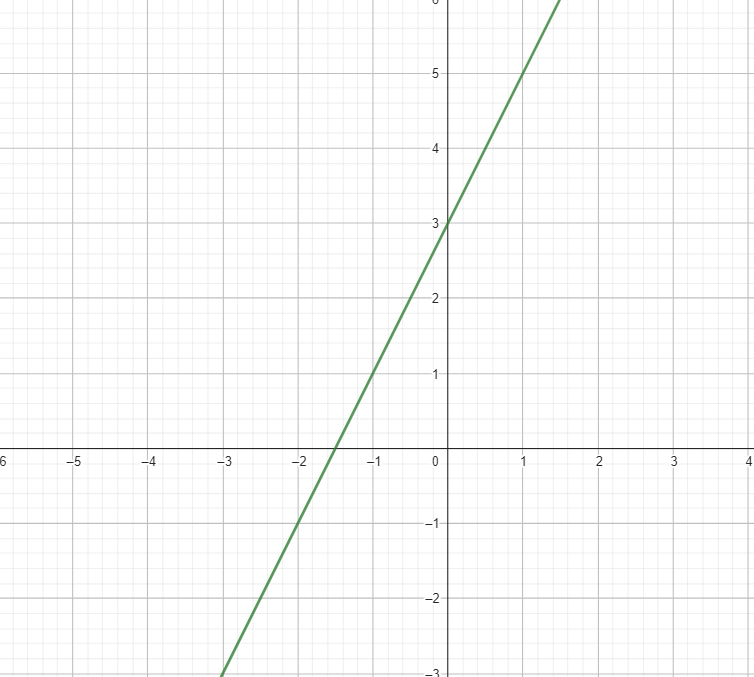
Graph the second line
y = -x + 1
(0, 1) and (1,0)
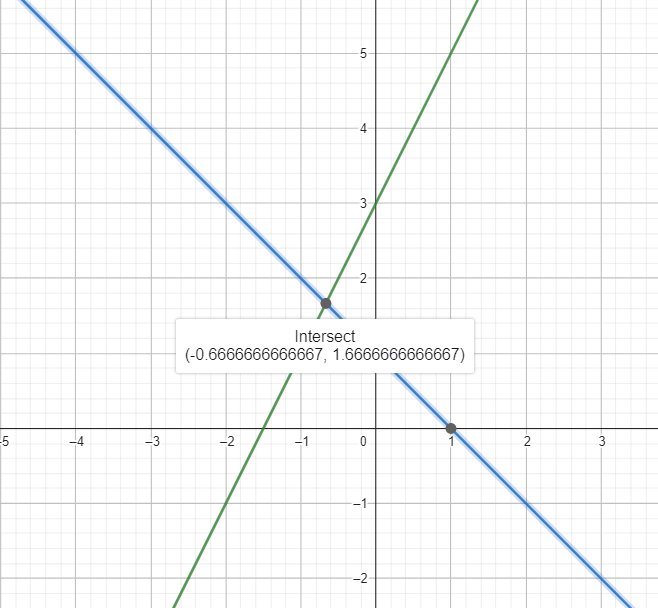
Find where the 2 lines intersect. You can get a rough estimate and then plug in the ordered pair to both equations to get an exact answer
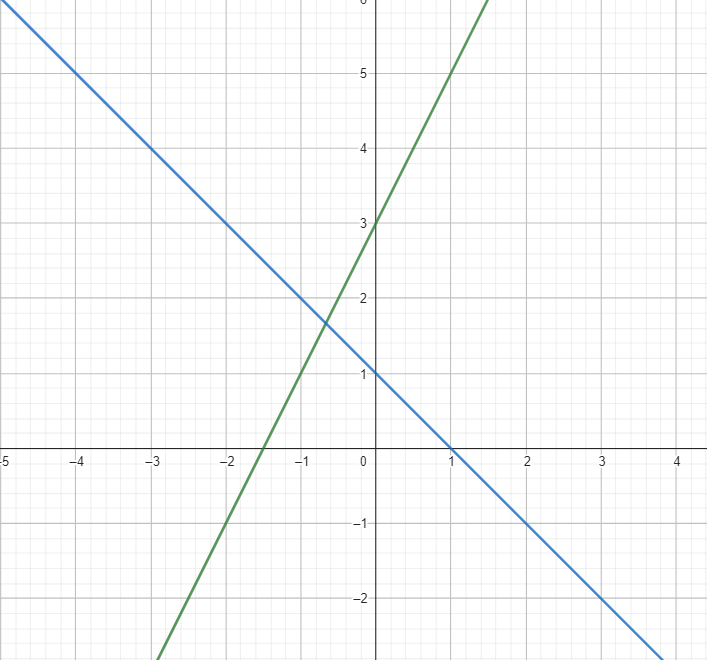
The lines look like they intersect at ([latex]\frac{-2}{3}[/latex],[latex]\frac{5}{3}[/latex])
Plug in both of these values into each equation to see if both are true
[latex]\frac{5}{3}[/latex] = 2([latex]\frac{-2}{3}[/latex]) + 3
[latex]\frac{5}{3}[/latex] = [latex]\frac{5}{3}[/latex]
First equation is true. Now for the second
[latex]\frac{5}{3}[/latex] = - ([latex]\frac{-2}{3}[/latex]) + 1
[latex]\frac{5}{3}[/latex] = [latex]\frac{5}{3}[/latex]
Both values are true, so this is the solution. Doublechecking on our graph we see