9.4 Homework Problems: Practical Applications of Logarithmic Functions
1. Cs-137 is used in the calibration of Geiger Counters. The half-life of Cs-137 is 30 years. If we start with at 10 g sample and it decays at a continuous rate of 2.3% per year
a. Write a function to model the decay of Cs-137
b. How much will be left after 5 years?
c. How much time will it take for the sample to reach 5 mg?
2. Newtons law of cooling is used by investigators to determine time of death. If a victim starts at 98.6 °F and it sits in a room that is consistently 60 °F how long will it take to cool to a temperature of 72.4 °F (k = 0.1947)?
T(t) = Ts + (T0 – Ts) e -k t (Newtons Law of Cooling)
3. The equation for the voltage across a capacitor during charging is given by
VC = VF + (Vi – VF) e(-t /RC)
a. If VF = 12 V, Vi = 0.1 V and RC = 0.72, find VC when t = 0.4 seconds
b. Find the amount of time it takes for the capacitor to have 10 V across it
4. Using the capacitor charging equation listed in question 3, look at the diagram below and answer the following questions
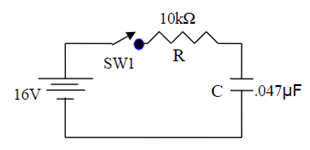
a. How long does it take the capacitor in the figure to charge to 11 V if it was initially uncharged (Vi = 0) ?
b. How long does it take the capacitor to charge to 11 V if the initial voltage was 3 V?
c. If the capacitor was initially uncharged, how much charge would it accumulate if the switch has been closed for 550 μs?
d. If the capacitor was initially charged to 2 V, determine the capacitor voltage after the switch has been closed for 300 μs?
5. In a laboratory study, the growth of E.Coli bacteria. You start with an initial culture of 100 E.Coli cells and observe that it grows at a continuous rate of 8% per hour.
a. How many E.Coli cells will there be after 2 hours?
b. How long will it take for the colony to reach 1,024,000 cells?
6. For the figure below, the capacitor is charged to 26 V, It will discharge when the switch is closed. If the switch is closed for 10 ms, how much charge will the capacitor have?
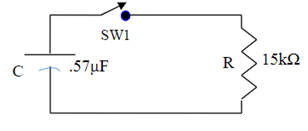
7. For the same circuit in problem 6, how log does it take for the capacitor to discharge to 12 V?
8. The decibel scale (dB) is used to measure sound “loudness” and is given by the equation
dB = 10 log (I)
Where dB is the measure of loudness and I is the ratio of sound intensity. If the measuring device you are using measures 82 dB, what is the ratio of sound intensity in pW/m2?
9. The magnitude of an earthquake is measured using the Richter Scale and is given by the following equation
R = log (I)
Where I is the intensity of the quake and R is the value on the Richter Scale.
a. The earthquake that struck Haiti in 2021 registered a 7.2 on the Richter Scale. What was the intensity of the quake?
b. In 2011 a magnitude 9.1 earthquake hit Japan, triggering the Fukushima Nuclear Disaster, what was the intensity of the quake?
c. The long beach earthquake in 1993 measured a 6.2 on the Richter Scale. Compare the intensities of the three earthquakes
10. Using the equation below, solve the following problems A certain power amplifier will give an increased output power Find the dB gain for the amplifier when:
Given: [latex]G_{dB}\ =\ 10\ log\ \left(\frac{P_{out}}{P_{in}}\right)[/latex]
a. The input is 60 W and the output is 800 W
b. The input is 20 W and the output is 1000 W
11. Geologists are studying a rock formation and want to determine its age by analyzing the decay of Uranium-238 (U-238) into Lead-206 (Pb-206). In a sample of the rock, they find that the concentration of U-238 is only 50% of what it would have been when the rock was first formed. Given that the half-life of U-238 is about 4.468 billion years, find the age of the rock
12. Given the formula [latex]y=\ y_oe^{0.5t}[/latex] which solves for the number of bacteria present after t days, where yo is the initial number of bacteria. How many days will it take for the number of bacteria to triple in number?
13. The general formula for radioactive decay is [latex]y=\ y_oe^{-kt}[/latex] . The half-life of a substance is the time needed for the substance to decay to ½ of the original amount. The half-life of radium-226 is 1600 years. If 50g (yo) are present today, how many grams will remain in 200 years. (Hint: First determine the value of k for radium-226.)
14. The current 𝑖 [latex]=6.25e^{-125t}[/latex] in a certain circuit is given by 𝑖(amps) where t is in time in seconds. At what time will the current be 1A?
15. The current though a charging capacitor is given by [latex]i=\ \frac{\ V}{R}e^{-\frac{t}{RC}}[/latex]; if V = 300V, R = 100Ω and C = 3100µF, find the time at which the current through the circuit equals 22mA.
16. A transmission line has a loss of 0.60 db with an output of 1400V. What is the voltage input given: [latex]G_V\ =\ 20\ log\ \left(\frac{V_{out}}{V_{in}}\right)[/latex]
17. Carbon dating is used to determine the age of organic material in Archeology. It uses carbon-14 which has a half life of 5730 years. If an archeologist finds a wooden tool that has 20% of the original amount of C-14, what is the approximate age of the fossil?