8.3 Homework Problems: Euler’s Number

1. Solve the following

a.  e^0.6

is this growth or decay?

b.  325e^-0.95

is this growth or decay?

2. A radioactive material is known to decay at 0.2 times the amount of material every year. You have 500 g of the material initially, how many grams will you have in 12 years? The function for this decay is A(t) = A0 e ^{– r t}

3.  Bacteria grows at a continuous rate of 9% per day. Find the final mass of a culture of bacteria after 6 days if there were 43 grams initially

4. Newtons law of cooling states that the rate of cooling an object is proportional to the temperature difference between the object and its surroundings.

T(t) = T_s + D₀ e^{-k t}

If k = 0.1947, T_s = 60 °F and D₀ = 38.6 °F find the temperature T(t) at t = 5 hours

5. A biologist has a 515-gram sample of a radioactive substance. Find the mass of the sample after two hours if it decreases according to a continuous exponential decay model, at a relative rate of 6% per hour.

6. The equation for the voltage across a capacitor is given by the function

V(t) = V­_F + (V­_i – V_F) e^-t/RC

Where V_F is the voltage across the capacitor at time t, V­_i is the initial voltage across the capacitor and t is time in seconds. R and C are the values of the resistor and capacitor in the circuit.

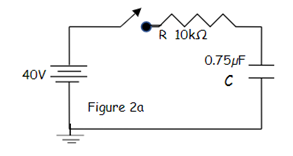
a.  If the capacitor is initially uncharged in figure 2a (V_i = 0), what will be the charge at t = 4 ms?

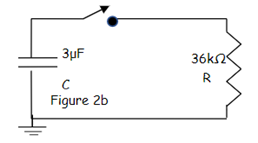
b.  If the capacitor in figure 2b was initially charged to 20 V, and will discharge when the switch is closed, what will the final charge be 100 ms after the switched is closed?

Unit 8.3 Printable Copy