8.2 Homework Problems: Exponential Functions and Half Life
1. Graph the following equation and draw its asymptote
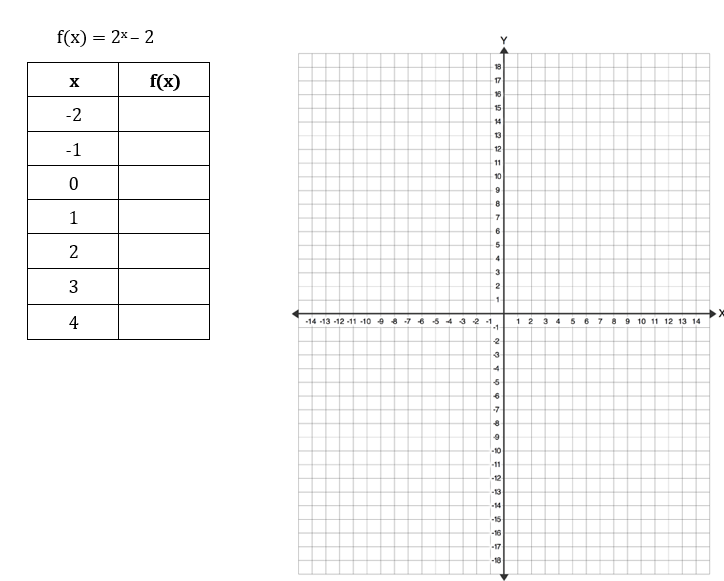
2. Define each as growth or decay
a. f(t) = 6000 (1 – 0.4)t
b. f(t) = 23,000 (1 + 0.2)–t
c. f(x) = 4 + 5(-x)
d. f(x) = 2 (x+3)
3. Bacteria will grow in a lab according to the function f(t) = y0 * 50.2t where y0 is the initial amount of bacteria and t is the amount of time in hours. How much bacteria will be present at the end of 5 hours if there were 5000 bacteria initially?
4. You earned $1500 and put it in a bank. Through the bank, that money earns 5% interest compounded annually. How much money will there be after 5 years if you don’t add any more to the account?
5. You buy a new truck with all that money you are making as a successful technician for $67,000. The value depreciates on that truck by a rate of 20% each year till the 5 year mark. How much is that truck worth at the end of 5 years?
6. A fish pond’s population is dying at an exponential rate. The pond started with 1046 fish in 2010, and every year the population decreases by 0.2%. How many fish were in the pond in 2018 to the nearest whole fish?
7. The half life of Zn-71 is 2.4 minutes. If you started out with 100.0 g of the material initially, how much would be left after 7.2 minutes?
8. Pd-100 has a half life of 3.6 days. If you had 6.02 x 1023 atoms a the start of your experiment, how many atoms would you have at 20 days?