Unit 7.1 Trigonometric Functions
Trigonometric Functions
Trigonometric functions are mathematical functions that relate the angles of a triangle to the lengths of its sides. These deal with triangles with 90 degree angles or "right triangles". These functions are fundamental in the study of periodic phenomena, such as waves and oscillations, and are widely used in various fields including physics, engineering, and computer science. The primary trigonometric functions are sine, cosine, and tangent, each of which has reciprocal functions: cosecant, secant, and cotangent, respectively.
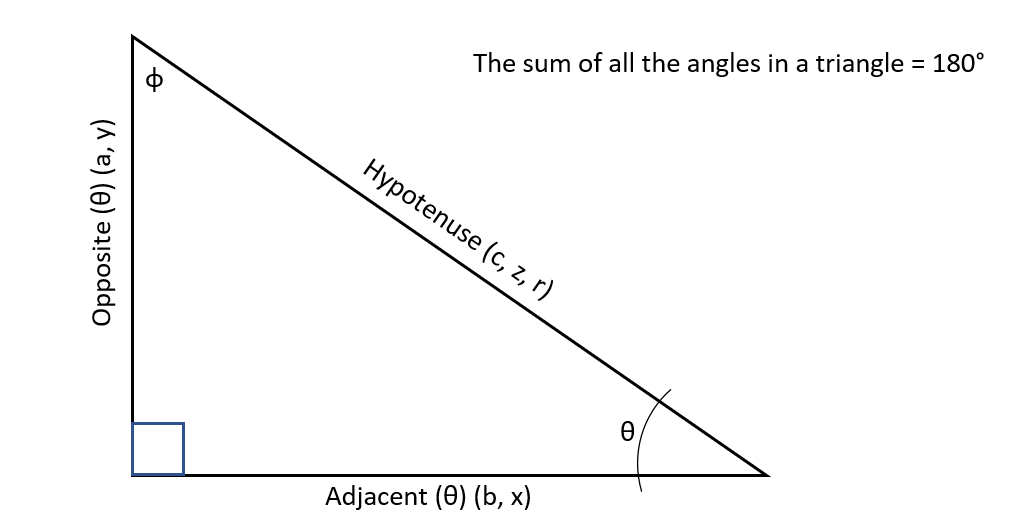
The sides of the triangle are defined by their location in respect to the labeled angle. For angle θ (theta) the side touching the angle that is not the hypotenuse is the adjacent side. The side not touching it is the opposite. The longest side of the triangle is the hypotenuse. It will always be opposite of the 90 degree angle (denoted by the square)
Sine
[latex]\sin{\theta}=\ \frac{opposite}{hypotenuse}[/latex]
Cosine
[latex]\cos{\theta}=\ \frac{adjacent}{hypotenuse}[/latex]
Tangent
[latex]\tan{\theta}=\ \frac{opposite}{adjacent}=\ \frac{\sin{(\theta)}}{\cos{(\theta)}}[/latex]
Cosecant
[latex]\csc{\theta}=\ \frac{hypotenuse}{opposite}[/latex]
Secant
[latex]\sec{\theta}=\ \frac{hypotenuse}{adjacent}[/latex]
Cotangent
[latex]\sec{\theta}=\ \frac{hypotenuse}{adjacent}[/latex]
Remember: SOH CAH TOA
SOH (sine is opposite over hypotenuse)
CAH (cosine is adjacent over hypotenuse)
TOA (tangent is opposite over adjacent)
Using the Inverse Functions (Arc Functions)
You use the inverse functions of the trig functions to "undo" them and solve for angles
[latex]\theta=\sin^{-1}{\left(\frac{opposite}{hypotenuse}\right)}[/latex]
[latex]\theta=\cos^{-1}{\left(\frac{adjacent}{hypotenuse}\right)}[/latex]
[latex]\theta=\tan^{-1}{\left(\frac{opposite}{adjacent}\right)}[/latex]
Pythagoreans Theorem
the sum of the squares on the legs of a right triangle is equal to the square of the hypotenuse
a2 + b2 = c2
Non - right Triangles
Not every triangle is a right triangle. You can solve for an angle or a side using Law of Cosines
c2 = a2 + b2 – 2 a b cos(θ)
Converting Between Radians and Degrees
In trigonometry, angles can be measured in two primary units: degrees and radians. Both units are used to describe the size of an angle, but they do so in different ways. Understanding the difference between radians and degrees is essential for solving problems in trigonometry, calculus, and other areas of mathematics.

Degrees
Degrees are a unit of measurement for angles that divide a full circle into 360 equal parts. Each of these parts is called a degree. This system of measurement is ancient and is believed to have originated from the Babylonians, who used a base-60 numbering system.
- One full circle: 360 degrees
- Half circle (straight angle): 180 degrees
- Quarter circle (right angle): 90 degrees
For example, an angle of 45 degrees represents 45 parts out of 360 parts of a full circle.
Radians
Radians are another unit of measurement for angles, based on the radius of a circle. One radian is defined as the angle created when the arc length is equal to the radius of the circle. This unit of measurement is more natural in higher mathematics, particularly in calculus, because it directly relates the angle to the properties of the circle.
- One full circle: 2π radians
- Half circle (straight angle): π radians
- Quarter circle (right angle): π/2 radians
Radians to Degrees
[latex]\deg{=}rad\ast\ \frac{180}{\pi}[/latex]
Degrees to Radians
[latex]rad{=}deg\ast\ \frac{\pi}{180}[/latex]