13.4 Homework Problems: Practical Applications of Systems of Equations

You are running a concession stand at a basketball game. You are selling hot dogs and sodas. Each hot dog costs $1.50 and each soda costs $0.50. At the end of the night you made a total of $78.50. You sold a total of 87 hot dogs and sodas combined. How many hot dogs were sold and how many sodas were sold that night?
Circuits can be analyzed using methods called “Mesh Current or Nodal Analysis”. It uses the principle of Kirchhoff’s Voltage Law and Kirchhoff’s Current Law. Using the following equations, find I1 and I2 (Ohms law : V = I * R). Use any method to solve

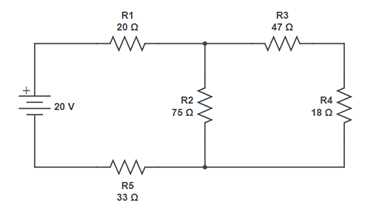
Vsource = ((R₁ + R₂ + R₅) * I₁) – ((R₂) * I₂) (eq.1)

(R₂* I₁) – ((R₂ + R₃ + R₄) * I₂) = 0 (eq.2)

Use the following equations and nodal analysis to solve for the voltages at node a (V_a) and b (V_b) in the circuit below. Use any method to solve

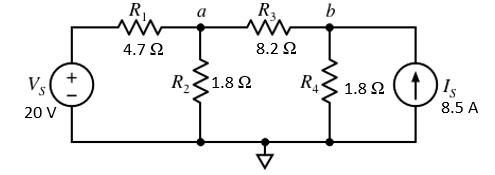
[latex]\frac{V_s-V_a}{R_1}=\frac{V_a}{R_2}+\frac{V_a-V_b}{R_3}[/latex] eq. 1

[latex]I_s=\frac{V_b}{R_4}+\frac{V_b-V_a}{R_3}[/latex] eq. 2

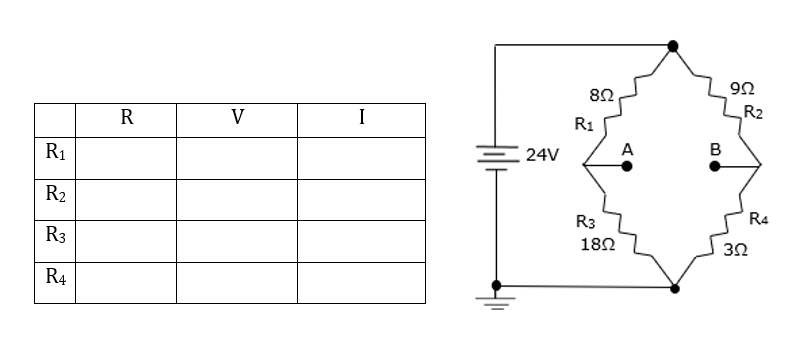
Use the following equations to solve for the voltages at nodes A (VA) and B (VB) in the circuit below. Fill out the table provided for all values using Ohms Law. Use any method to solve.

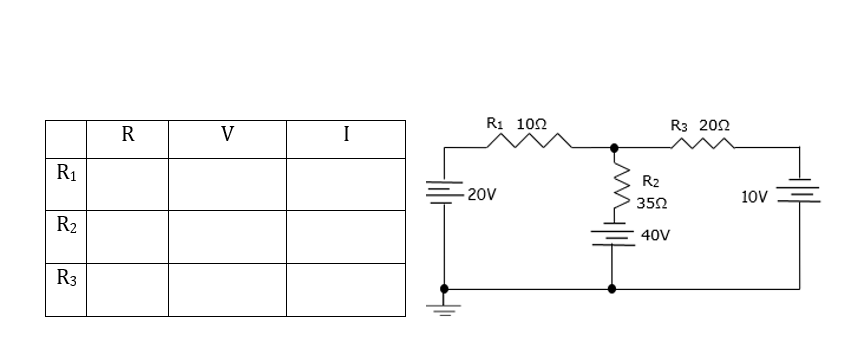
Use the following equations to solve for values in the circuit. Fill out the table provided for all values using Ohms Law. Use any method to solve.

Your friend rides the ski lift to the top of a run at Pebble Creek, which is a distance of 1.75 km. He skis directly down the hill at a rate of 5 times faster than the lift travels. The total time (between the lift and skiing down) was 45 minutes. Find the rate it takes him to ski down the hill (in km per hour)

Plane A travels 450 miles per hour. Plane B travels 500 miles per hour. If Plane A takes 25 minutes longer to travel a distance (d) than Plane B, find the distance (d) they are traveling

A motorboat leaves the harbor and travels at an average speed of 15 km/hr towards an island. The average speed on the return trip was 10 km/hr. How far was the island if the trip took a total of 5 hours?

Joey and Natasha start from the same point and walk in opposite directions. Joey walks 2 km/hr faster than Natasha. After 3 hours, they are 30 km apart. How fast did each person walk?

License