Unit 4.5 Linear Inequalities
Linear Inequalities
Linear inequalities are similar to linear equations but instead of an equals sign, a inequality symbol takes its place.
Example: 3x + 6 < y
When solving a linear inequality for a variable, treat the inequality as an equal sign. It is important to remember that when you divide by a negative number, the sign flips
The main difference between graphing a linear inequality and a linear equation is that you will shade the area that corresponds to the inequality. You look at all y values that are greater than/ less than and shade the area. Also when working with inequalities, you can have a dashed line, or a solid line and both mean different things.
A solid line indicates that it is less than/greater than or equal to. For the inequality y ≥ x + 1
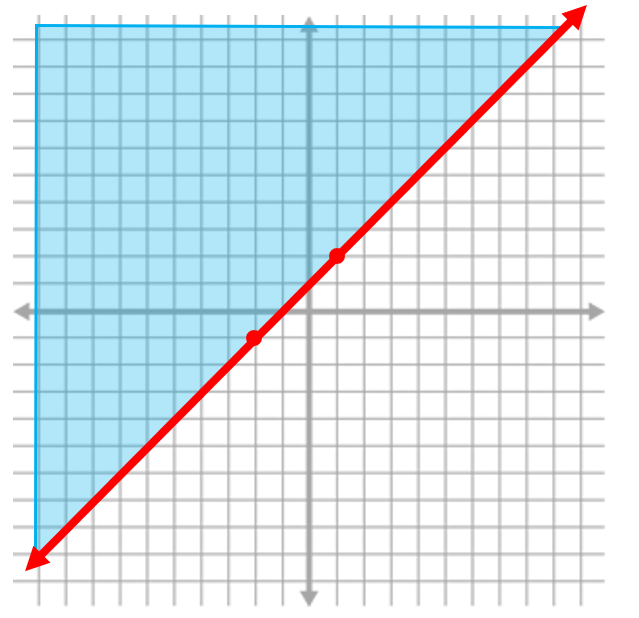
A dashed line indicates that y is less than/ greater than. For the inequality y > x + 1
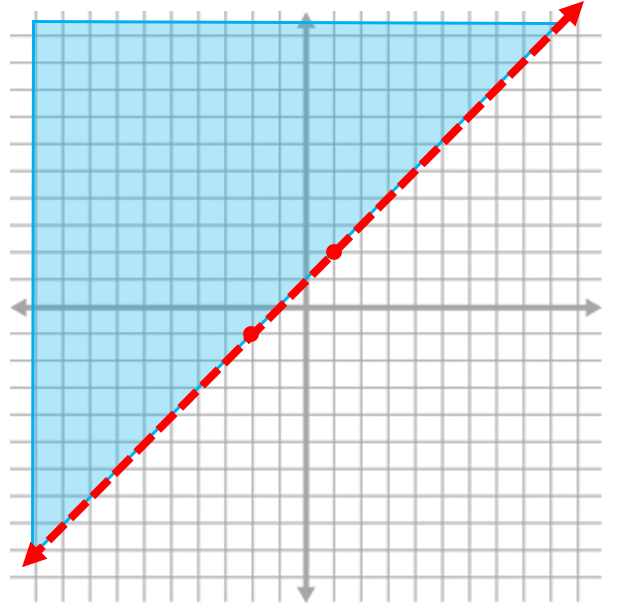
Both of these are shaded so that it includes all values of y that are greater than the line, but one is dashed and one is solid.
Solving a linear inequality
Write the linear inequality 9x – 3y ≥ 6 in slope intercept form then graph the line
First thing to do is to get y by itself so it can be written in slope intercept form
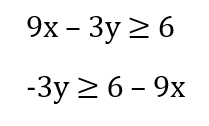
Subtract 9x from both sides
Next divide by -3
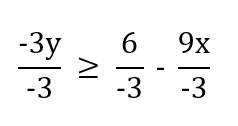
You have to do this to all terms on both sides of the equation.
Because you are dividing by a negative number, you must flip the sign. It is now y is less than or equal to the right hand side of the equation
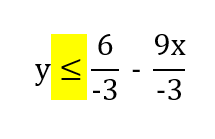
Simplifying further we get
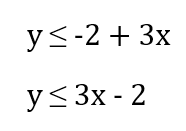
y ≤ 3x – 2
To graph this line, it is the same process as graphing a linear equation. Find two points and draw the line
Two points that fall on this line are (-1, -5) and (2,4)
In this example, it is all y values that are less than the line 3x – 2. Therefore we look at the y axis and determine values that are less than the line
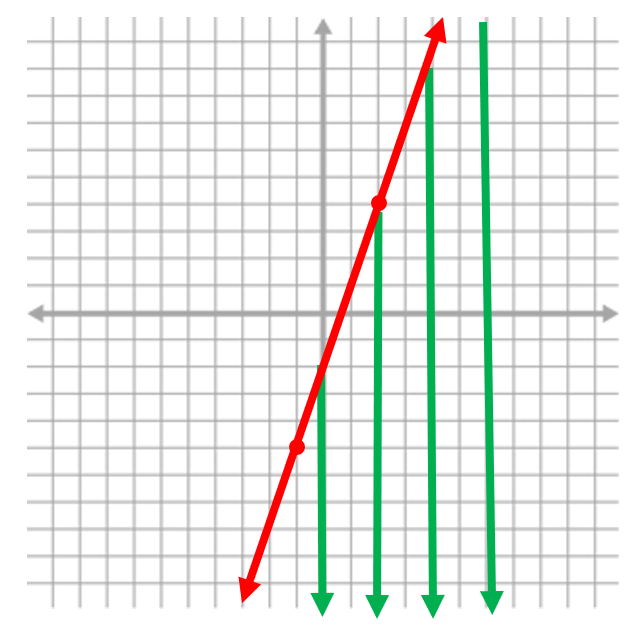
The green arrows indicate the direction that we will shade because those are the y values that are less than our line (hint, look at the y axis). We are looking at ALL y values that are less than the line so we add a shaded area to include all values
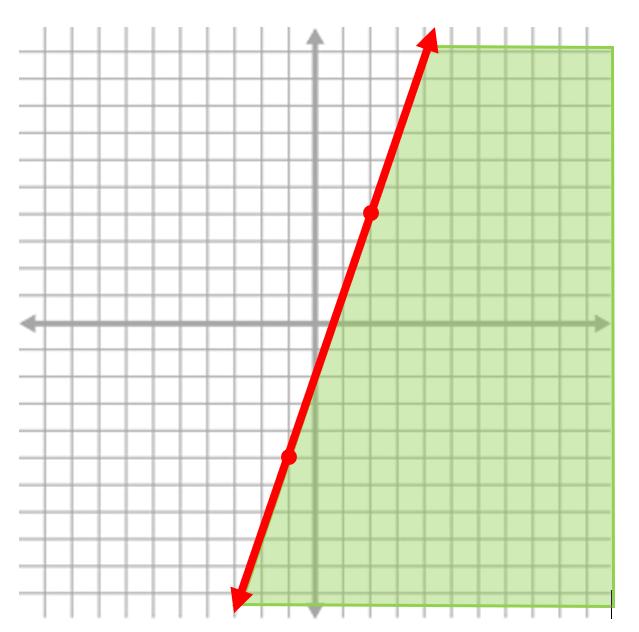
This includes all possibilities of y values that are less than or equal to the line y = 3x – 2. Because y is less than or equal to, the line is solid.